Математическая логика и теория алгоритмов
20 рублей за вопрос
Письма присылайте на Почтовый ящик
1. Степень истинности или степень ложности каждого нечетного высказывания принимает значение:
2
1
[0,1]
0
2. Исчисление высказываний будем считать полным в широком смысле, если:
В ней доказуема каждая формула, являющаяся тавтологией;
В ней доказуема только одна из формул являющееся тавтологией;
В ней нет доказуемых формул являющихся тавтологией;
В ней доказуема только одна из формул.
3. Выберите правильный вариант:
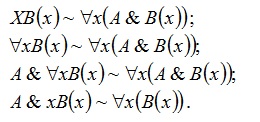
4. Выражение А&В => С╞ А => (В => С) − это правило:
Заключения;
Отрицания;
Соединения посылок;
Разъединения посылок.
5. Иногда литералы или дизъюнкты называют:
Сколемовскими функциями;
Клаузами;
Литералом;
Дизъюнкцию литералов.
6. Отдельная аксиома дедуктивной теории, называется независимой, если:
Аксиому можно вывести из остальных аксиом;
Аксиому можно вывести только из одной аксиомы;
Аксиому можно вывести в этой теории но не из остальных аксиом;
Аксиому нельзя вывести в этой теории из остальных аксиом.
7. Эквивалентность это:
Логическая операция, с помощью которой из двух данных высказываний А и В образуется новое высказывание, обозначаемое А&В, которое истинно тогда и тогда, когда А и В оба истинны;
Логическая операция, с помощью которой из двух данных высказываний А и В образуется новое высказывание, обозначаемое А=В, которое истинно тогда и тогда, когда А и В принимают одинаковые истинностные значения;
Логическая операция, с помощью которой из двух данных высказываний А и В образуется новое высказывание, обозначаемое А=>В, которое ложно и тогда, когда посылка А истинна, а значение В ложно;
Логическая операция, с помощью которой из двух данных высказываний А и В образуется новое высказывание, обозначаемое А˅В, которое ложно тогда и только тогда, когда ложны оба высказывания А и В.
8. Временная сложность вычислений (алгоритма) характеризует:
Число операций для решения задачи заданного размера;
Сложность операций для решения задачи заданного размера;
Значения операций для решения задачи заданного размера;
Длина операций для решения задачи заданного размера.
9. В двузначной логике отрицание лжи есть:
Ложь;
Отрицание;
Истина;
Неопределенность.
10. Полуэффективным процессом считается:
Некоторый алгоритм;
Некоторый процесс;
Заданный алгоритм;
Некоторая процедура.
11. Выражение А&В ├ А – означает правило:
Удаления &;
Перевёртывания;
Сведения к нелепости;
Введения.
12. Стратегия вычеркивания будет полной, если:
Использовать ее отдельно от метода насыщения уровней;
Использовать ее вместе с методом насыщения уровней;
Использовать с другим методом;
Использовать как отдельно так и вместе с методом насыщения уровней.
13. Функцию μА*(х) называют:
Функцией равенства;
Теоремой;
Аксиомой;
Функцией принадлежности.
14. Если существует такая подстановка и, что (L1)Ѳ = (L2)Ѳ = … = (Ln)Ѳ тогда множество литералов называется:
Унифицируемым;
Алгоритмом унификации;
Литералом;
Унификатором.
15. Исчисление предикатов 1-го порядка называется полным в широком смысле, если:
Каждая логическая общезначимая формула является тавтологией;
Каждая логическая общезначимая формула не является теоремой;
Каждая логическая общезначимая формула является теоремой;
Каждая логическая общезначимая формула не является аксиомой.
16. Число необходимых сравнений можно уменьшить, если использовать принцип:
«Разделяй»;
«Разделяй» и «властвуй»;
Простых итераций;
«Властвуй».
17. Укажите правило введения ˅:
18. Символ Ɐх называется:
Числовым индексом;
Квантором всеобщности;
Функцией;
Квантором существования.
19. Задача называется NP – трудной если:
Каждая задача из NP полиномиально сводится к ней;
Одна задача из МР полиномиально сводится к ней;
Любая задача КР сводится к ней;
Каждая задача из NP не сводится полиномиально к ней.
20. Подстановку Θ называют:
Унифицируемым;
Литералом;
Унификатором;
Алгоритмом унификации.
21. Методом резолюций называется:
Получение значений из данных конъюнктов и вновь получаемых конъюнктов;
Последовательное получение бинарных резольвент из данных дизъюнктов и вновь получаемых дизъюнктов;
Получение значений из формул;
Последовательное получение бинарных значений.
22. Дизъюнкт D называется поддизъюнктом D* (или D поглощает D*):
Если D является некоторой частью дизъюнкта D*;
Если D не является некоторой частью дизъюнкта D*;
Если D является конъюнктом;
Если D > D*
23. Императивную (процедурную) вычислительную модель называют:
Когда имеется последовательная система значений;
Когда имеется система цифр;
Когда имеется последовательная система команд;
Когда не имеется последовательная система команд;
24. На рисунке представлено:
Дерево родственных отношений;
Отношения связей;
Множество родственных связей;
Зависимость отношений.
25. Формула А ˅ В выполнима в данной интерпретации когда:
В этой интерпретации истинно А;
А и В принимают значение И одновременно или значение Л;
А истинно в этой интерпретации, а В ложно;
Хотя бы одна из них выполнима в этой интерпретации.
26. Пропозициональные формы А и В называются равносильными, если:
При каждой совокупности значений, формы принимают различные истинностные значения;
При каждой совокупности значений, формы принимают одинаковые истинностные значения;
При каждой совокупности значений, формы принимают различные ложные значения;
При каждой совокупности значений всех пропозициональных букв, входящих в А и В, эти формы принимают одинаковые истинностные значения.
27. Буквы конца латинского алфавита (х,y,z,…) и они же с числовыми индексами (x1,x2,…,y1,y2,…,z1,z2,…) называются:
Свободными переменными;
Функциональными буквами;
Предметными постоянными;
Предметными переменными.
28. Выражение А => (В => C) ╞ A&B => C – это правило:
Отрицания;
Заключения;
Соединения;
Контрапозиции.
29. Буквы конца латинского алфавита (a,b,c,…) и они же с числовыми индексами (a1,a2,…,b1,b2,…,c1,c2,…) называются:
Предметными переменными;
Предметными постоянными;
Функциональными буквами;
Свободными переменными.
30. Литера называется негативной, …:
Если она не содержит отрицания;
Если она равносильна;
Если она выполнима;
Если она содержит отрицания.